1. Autofocusing-based correction of B0 fluctuation-induced ghosting

Long-TE gradient-echo images are prone to ghosting artifacts. Such degradation is primarily due to magnetic field variations caused by breathing or motion. The effect of these fluctuations amounts to different phase offsets in each acquired k-space line. A common remedy is to measure the problematic phase offsets using an extra non-phase-encoded scan before or after each imaging readout.

We attempt to correct for constant phase errors in spin-warp imaging as well as for constant and linear phase errors in EPI by estimating the phase offsets directly from the raw image data using an autofocusing approach. Autofocusing (AF) methods belong to the class of retrospective reconstruction techniques, and are well-studied in the context of motion correction. We tackle the phase correction problem with an optimization-based search of phase correction factors. Such search relies on an objective function with differentiable terms that is sensitive to the phase-related ghosting artifacts. We seek the latent phase offsets that are associated with a minimal value of the image quality measure that is evaluated in the spatial domain. This way we avoid the need for extra navigator scans and the related increase in sequence complexity and scan time. Furthermore, we propose and explore two distinct objective functions that can be used to correct for phase artifacts in the scans acquired with parallel imaging and acceleration. The experimental results demonstrate that our method is capable of minimizing the ghosting artifacts and that the quality of the output images is similar to navigator-based reconstructions.

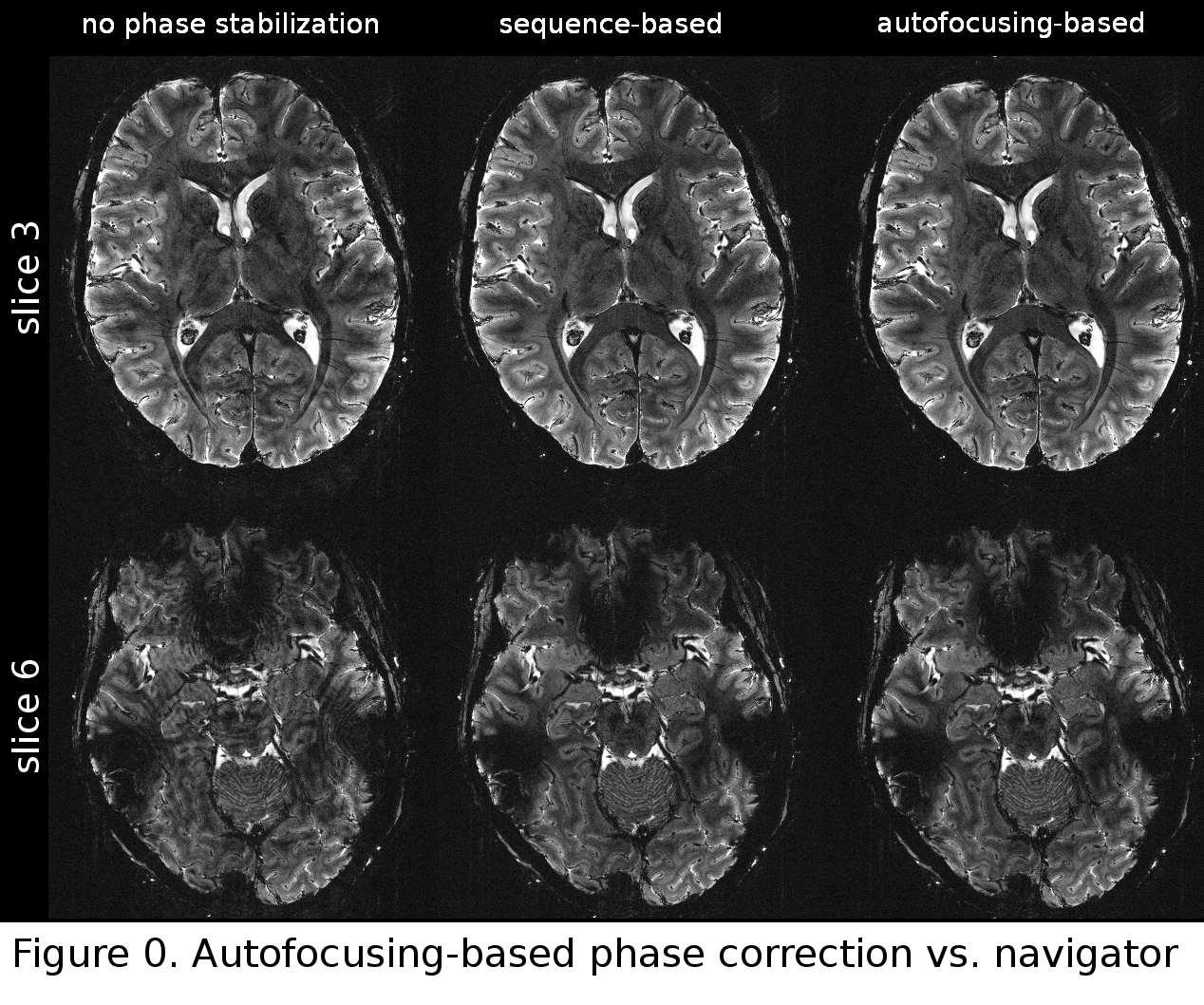
Figure 0 shows a comparison between uncorrected images with images corrected for B0 fluctuations using a conventional navigator-based approach as well as the proposed autofocusing-based method. Ghosting artifacts in the uncorrected data are more severe in slice 6 (shown on the bottom), which is positioned lower than slice 3 (top). In both slices, autofocusing and navigator-based correction techniques are able to significantly improve image quality. Apart from some flow-related artifacts, ghosting is completely removed and the images resulting from both techniques are practically indistinguishable from one another.

2. Blind retrospective rigid motion correction

In recent years, most successful motion correction techniques have been based on prospective motion correction. However, prospective methods have certain limitations, which make their use not possible in certain scenarios. The goal of this project is to develop a new retrospective motion correction algorithm that does not require tracking equipment, and can be applied to already acquired data in a post-processing way. Quite importantly, as opposed to prospective techniques the method preserves the original motion corrupted image, which allows to compare the motion correction results with original image.

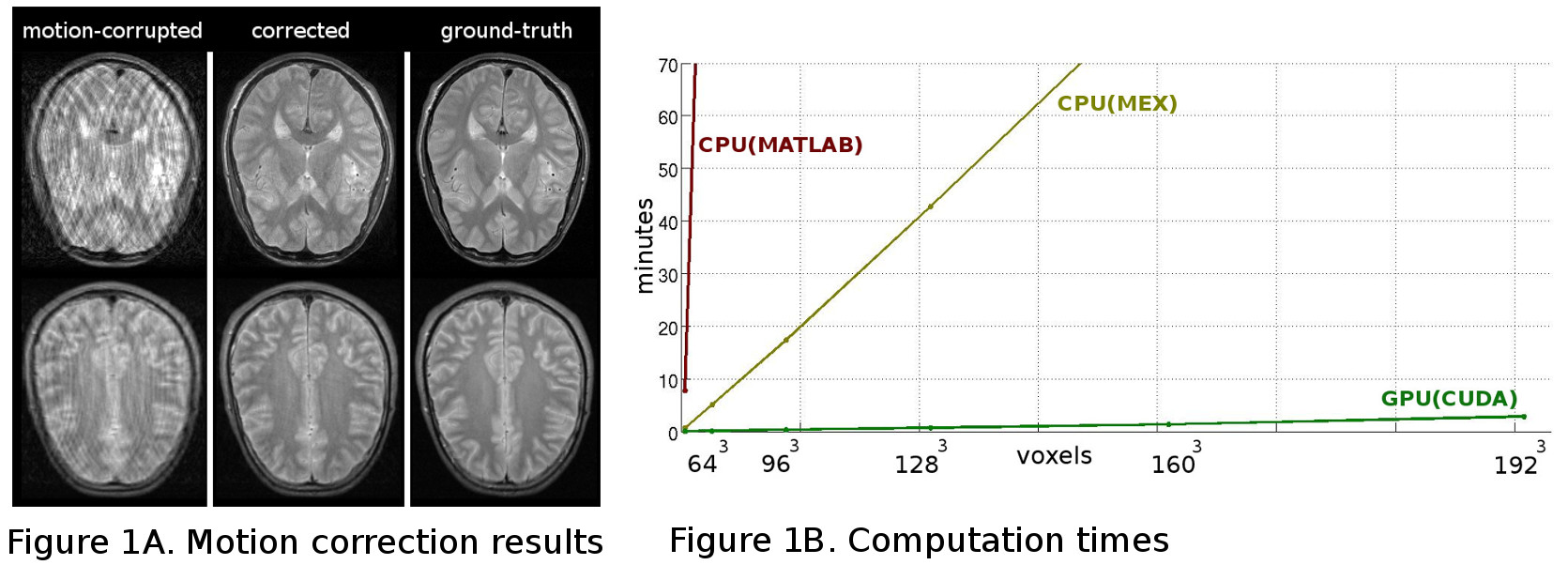
The current autofocusing-based retrospective methods suffer from the problem of being too slow to be used in the clinical practice. This is because the space of motion parameters is explored in a brute force inefficient way leading to highly suboptimal solutions or long computation times in high-resolution 3D scenarios due to the curse of dimensionality. Together with my colleagues I propose an autofocusing method that is based on a minimization of a cost function that characterizes the quality of the optimized image. The idea is to find the point in the space of possible motions such that the motion corrected image yields the minimum value of a cost function. The challenge for our approach is the fact that for high-resolution 3D volumes the optimization space is vast since there are 6 free parameters per phase encode step. We address this problem by using an analytic model for both motion degradation and its inverse, which allows to find the partial derivatives (gradients) of our cost function, and do an efficient optimization of the objective. For this reason we call our algorithm GradMC (Gradient-based Motion Correction). GradMC starts with an initial estimate of the motion trajectory (which can be no-motion indicating zeros or some small random values), and iteratively corrects for translation and rotation until no more progress in terms of image quality can be made. The image quality metric that we use in our cost function is the entropy of spatial image gradients (first finite derivatives).

We have developed a GPU version of GradMC featuring a parallel implementation of our forward model. For volumes of matrix sizes commonly encountered in clinical practice, only a few minutes are needed for the reconstruction (see Figure 1B). GradMC can correct for arbitrary motion trajectories in 6 degrees of freedom for both 2D and 3D acquisitions. Shown in Figure 1A are the motion correction results on a pair of 2D images acquired with a RARE sequence (matrix size N=384×160).

The Matlab implementation of GradMC along with 4 examples is available at: http://mloss.org/software/view/430/

3. Blind retrospective non-rigid motion correction

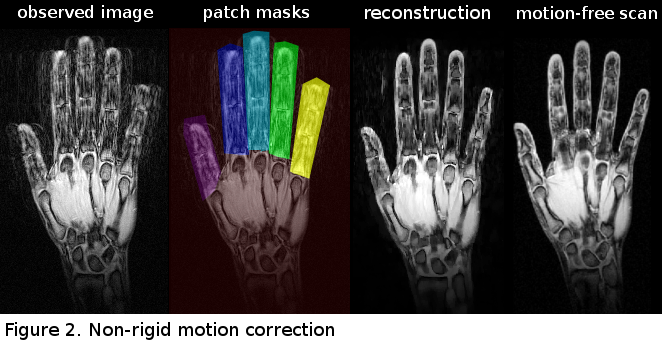
This project is an extension of the blind retrospective motion correction method aimed at correction of the non-rigid motion. Once again, the proposed method is purely image data-driven meaning that the motion correction algorithm (called GradMC2) does not require information about motion from external sensors as input. Being able to do such a reference-free correction in case of complicated spatially-varying motion is the main contribution we make with current work. The method can be used with generic acquisition sequences, and is associated with a reasonable computation time. We approximate non-rigid motion by locally (patch-wise) rigid motions, and extend the forward model to accommodate this “multi-rigidness” assumption. The method is autofocusing-based, which means that at the core is a generic image quality functional. Given the high complexity of the problem to be solved, and large number of unknowns it is crucial to be able to come up with an efficient optimization algorithm to recover both the underlying sharp image and local displacements characterized by distinct sets of motion parameters specified for each patch. We come up with an annealing-based alternating optimization procedure, where we benefit from the closed form formulation of our forward model in order to do efficient optimization using derivatives of the quality functional with respect to both latent image and motion parameters.

As an ultimate goal we see our method to be applied in routine clinical imaging, where the scans are affected by non-rigid physiological motion (e.g. in abdominal scans). In this study, we make a step forward towards this goal, and in our in vivo experiments we correct for multi-rigid finger motion in a wrist imaging setup (see Figure 2), which can be seen as a reasonable simplification of the realistic non-rigid problem.

4. FID-guided retrospective motion correction of accelerated data

Although advances in parallel imaging techniques allow reducing the scan time significantly, it still remains in the order of minutes, increasing the probability of head motion to occur. Motion during the acquisition leads to inconsistent k-space data and thus impedes parallel imaging reconstruction techniques, such as GRAPPA. On the other hand, Fourier domain-based retrospective motion correction techniques typically require a fully acquired k-space as input, and thus necessitate the GRAPPA reconstruction to be performed first. This couples the problems of motion correction and GRAPPA reconstruction, yielding a complex problem to solve.

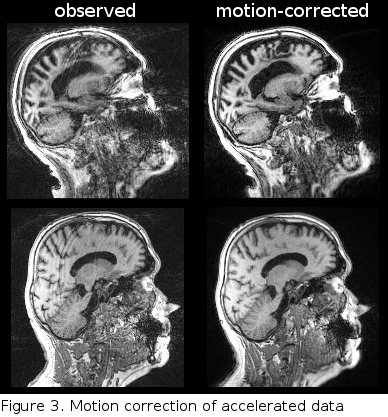
This project aims at developing of a prototype motion correction algorithm that operates on multi-channel undersampled data acquired with a Cartesian sequence which was augmented by a free induction decay navigator motion monitoring module. The algorithm is based on iterating the application of the GRAPPA reconstruction, motion estimation and motion correction. The acquired FIDnavs which were recently shown to be beneficial for retrospective motion correction were used to aid the motion correction process. The preliminary motion correction results are shown in Figure 3.

Employment:

Max Planck Institute for Biological Cybernetics - Tübingen, Germany

• 2015–present
• Research scientist

Education:

Max Planck Institute for Intelligent Systems - Tübingen, Germany

• 2011–2015
• Graduate student

Max Planck Institute for Biological Cybernetics - Tübingen, Germany

• 2009–2011
• Graduate student

Universität Osnabrück

• 2007–2009
• M. Sc. in Cognitive Science
• Focus: Neuroinformatics/Robotics

Volgograd State Pedagogical University - Volgograd, Russia

• 2001–2005
• B. Sc. in Physics
• Focus: Development of Physics educational software