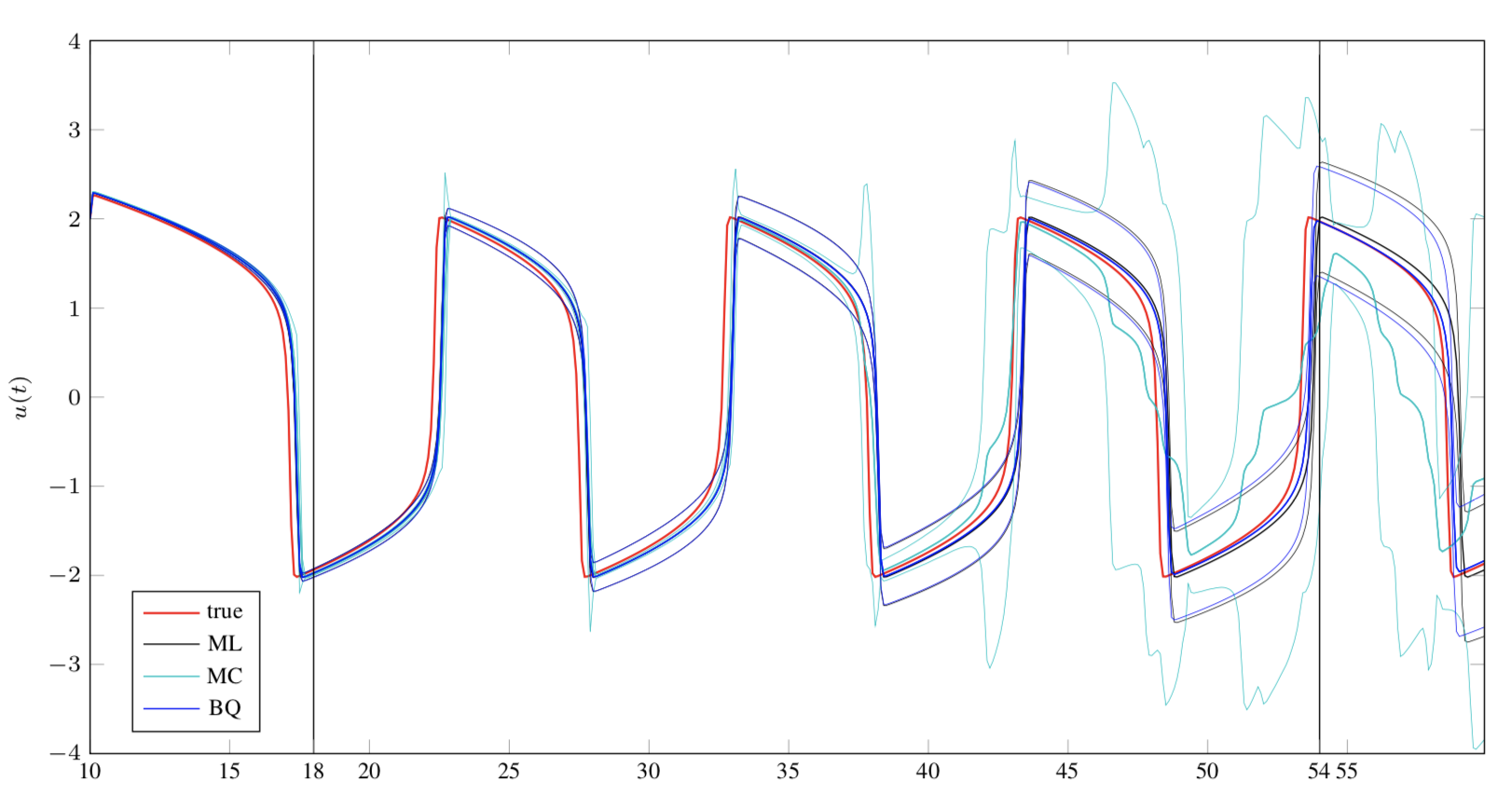
There is resurging interest, in statistics and machine learning, in solvers for ordinary differential equations (ODEs) that return probability measures instead of point estimates. Recently, Conrad et al.~introduced a sampling-based class of methods that are `well-calibrated' in a specific sense. But the computational cost of these methods is significantly above that of classic methods. On the other hand, Schober et al.~pointed out a precise connection between classic Runge-Kutta ODE solvers and Gaussian filters, which gives only a rough probabilistic calibration, but at negligible cost overhead. By formulating the solution of ODEs as approximate inference in linear Gaussian SDEs, we investigate a range of probabilistic ODE solvers, that bridge the trade-off between computational cost and probabilistic calibration, and identify the inaccurate gradient measurement as the crucial source of uncertainty. We propose the novel filtering-based method Bayesian Quadrature filtering (BQF) which uses Bayesian quadrature to actively learn the imprecision in the gradient measurement by collecting multiple gradient evaluations.
| Author(s): | Kersting, H. and Hennig, P. |
| Book Title: | Proceedings of the 32nd Conference on Uncertainty in Artificial Intelligence (UAI) |
| Pages: | 309--318 |
| Year: | 2016 |
| Month: | June |
| Editors: | Ihler, Alexander T. and Janzing, Dominik |
| Project(s): | |
| Bibtex Type: | Conference Paper (conference) |
| Event Place: | New York, USA |
| State: | Published |
| URL: | http://www.auai.org/uai2016/proceedings/papers/163.pdf |
| Electronic Archiving: | grant_archive |
BibTex
@conference{KerHen16,
title = {Active Uncertainty Calibration in Bayesian ODE Solvers},
booktitle = {Proceedings of the 32nd Conference on Uncertainty in Artificial Intelligence (UAI)},
abstract = {There is resurging interest, in statistics and machine learning, in solvers for ordinary differential equations (ODEs) that return probability measures instead of point estimates. Recently, Conrad et al.~introduced a sampling-based class of methods that are `well-calibrated' in a specific sense. But the computational cost of these methods is significantly above that of classic methods. On the other hand, Schober et al.~pointed out a precise connection between classic Runge-Kutta ODE solvers and Gaussian filters, which gives only a rough probabilistic calibration, but at negligible cost overhead. By formulating the solution of ODEs as approximate inference in linear Gaussian SDEs, we investigate a range of probabilistic ODE solvers, that bridge the trade-off between computational cost and probabilistic calibration, and identify the inaccurate gradient measurement as the crucial source of uncertainty. We propose the novel filtering-based method Bayesian Quadrature filtering (BQF) which uses Bayesian quadrature to actively learn the imprecision in the gradient measurement by collecting multiple gradient evaluations.},
pages = {309--318},
editors = {Ihler, Alexander T. and Janzing, Dominik},
month = jun,
year = {2016},
slug = {kerhen16},
author = {Kersting, H. and Hennig, P.},
url = {http://www.auai.org/uai2016/proceedings/papers/163.pdf},
month_numeric = {6}
}

