Adaptive Locomotion of Soft Microrobots
Networked Control and Communication
Controller Learning using Bayesian Optimization
Event-based Wireless Control of Cyber-physical Systems
Model-based Reinforcement Learning for PID Control
Learning Probabilistic Dynamics Models
Gaussian Filtering as Variational Inference
Learning Probabilistic Dynamics Models
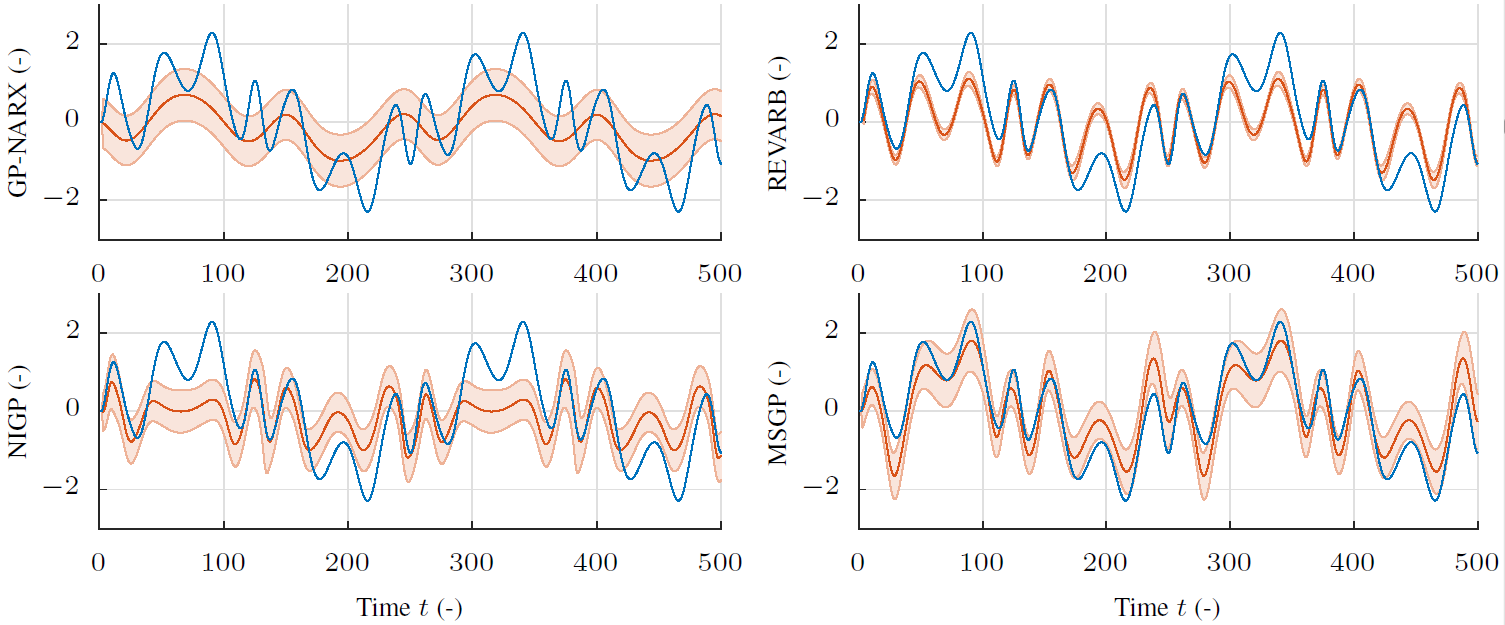
In Reinforcement Learning (RL), an agent strives to learn a task solely by interacting with an unknown environment. Given the agent’s inputs to the environment and the observed outputs, model-based RL algorithms make efficient use of all available data by constructing a model of the underlying dynamics. Data-efficiency has been shown to greatly improve over model-free (e.g. policy gradient) or value function based methods. At the same time, incorporation of uncertainty is essential to mitigate effects of sparse and non-iid data and to prevent model bias.
Learning probabilistic predictive models from time-series data on real systems is however a challenging task, for example, because of imperfect data (e.g. noise and delays), unobserved system states, and complex, non-linear dynamics (e.g. joint friction and stiction). This research aims for high quality, probabilistic, and long-term predictive models, in particular for the use in RL.
In [], we exploit three main ideas to improve model learning by leveraging structure from the subsequent RL problem:
- Optimize for long-term predictions.
- Restrict model learning to the input manifold reachable by the specific policy.
- Incorporate the approximations made for computing the expected discounted cost into the model learning.
The proposed model learning framework Multi Step Gaussian Processes (MSGP) [] was shown to enable robust, iterative RL without prior knowledge on a real-world robotic manipulator. At the same time, state-of-the-art predictive performance is demonstrated in a benchmark of synthetic and real-world datasets [
].
Oftentimes in practice, the underlying system state cannot be directly measured, but must be recovered from observed input/output data. In our work on Probabilistic Recurrent State-Space Models (PR-SSM) [], we lift ideas from deterministic Recurrent Neural Networks (RNN) into the realm of probabilistic Gaussian Process State-Space Models (GP-SSMs). The resulting inference scheme is derived as approximate Bayesian inference using variational techniques to robustly and scalably identify GP-SSMs from real-world data.
Members
Publications


