In recent years, theory has driven several architectural advances in deep learning, from improved design strategies of fundamental building blocks to analyses of gradient and signal propagation issues. Our approach provides a tight link between architecture and optimization dynamics: most effective deep architectures are the ones where gradients can flow the easiest and Hessian is well-conditioned.

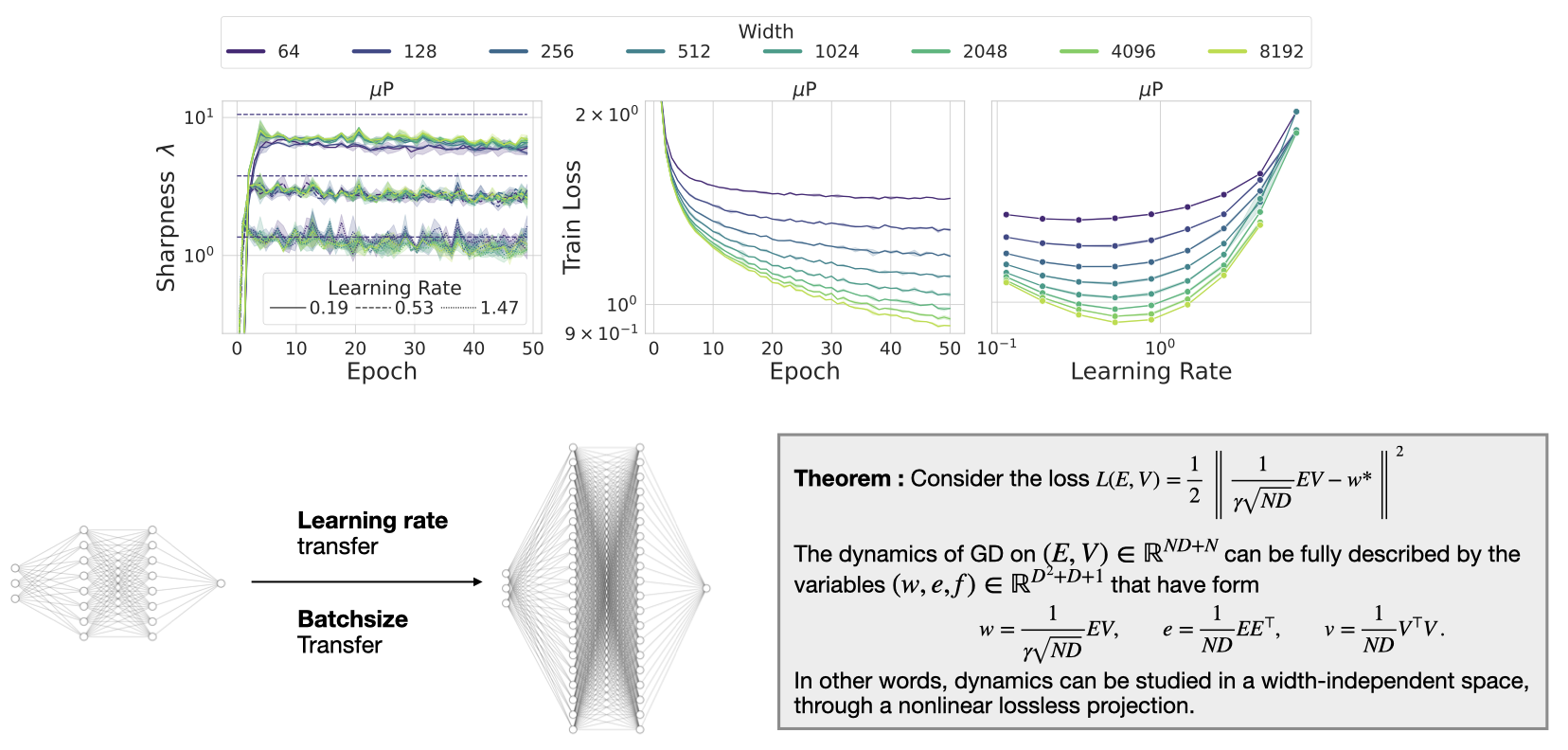
Sizeable attention in the literature was recently placed on the concept of hyperparameter transfer, tackling the following important question: Since training large-scale models is expensive, can we guarantee optimality with respect to the training hyperparameters by studying the dynamics of smaller networks? The answer to this question seems to be positive and resulted from the development of the so-called feature learning scaling limits (maximal update parametrization, dynamic mean field theory, etc.). In our recent publication [], we provide a tight link between optimization and feature learning, proving for the first time how network reparametrization can induce width-invariant dynamics. In addition, our result provide strong experimental evidence of how hyperparameter transfer can be linked to curvature of the optimization landscape. 
Another critical and conceptually similar question is how to optimally adjust hyperparameters after scaling the training process to a bigger cluster of GPUs. Our recent theoretical paper [] shows how to adapt momentum parameters and weight decay of adaptive optimizers, such as AdamW, as one scales up the batch size (i.e., number of devices). Our approach is based on stochastic differential equations and rooted in some gradient noise assumptions. Our future efforts will be devoted to empirical verification of our assumptions and to studying the effects of scheduling hyperparameters.