Multi-Objective Learn-to-Defer: Possibility, Complexity, and a Post-Processing Framework
Machine learning algorithms are increasingly applied in critical areas such as medical diagnostics and prognosis prediction, where human oversight is often necessary. Learn-to-Defer (L2D) is an emerging paradigm in which machine learning models abstain from making uncertain decisions, deferring them to human experts. Most existing L2D methods focus on optimizing overall accuracy but fail to address the multi-objective nature of real-world problems, which require balancing accuracy, safety, fairness, and human intervention costs. While some studies have tackled specific instances of multi-objective L2D problems, a general framework has remained elusive.
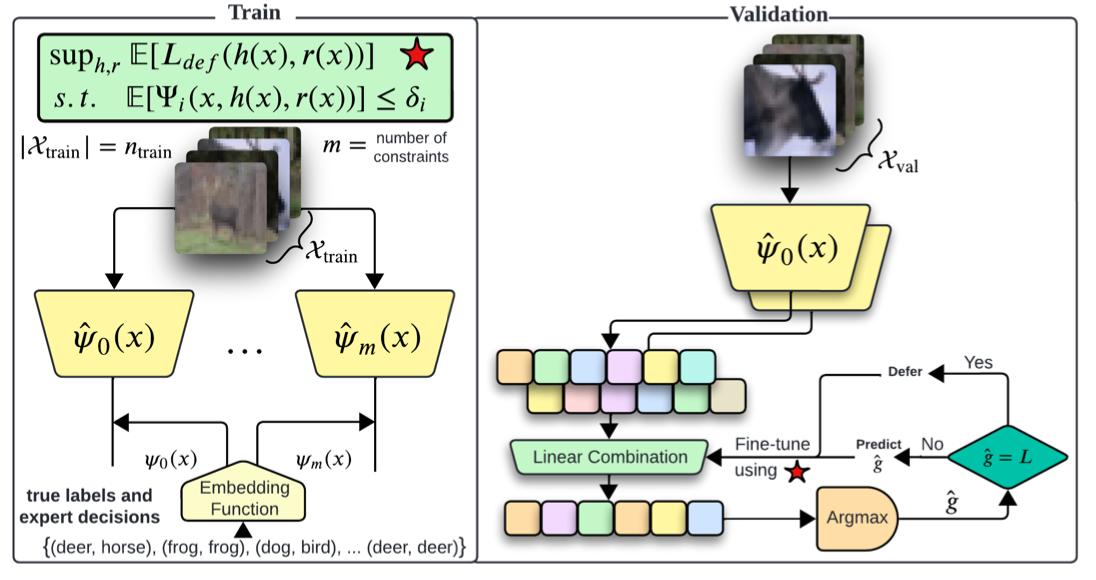
Recent advancements suggest that post-processing techniques provide an effective way to handle these multi-objective challenges, particularly in algorithmic fairness. These methods first estimate probability scores using learning algorithms and then optimize predictors based on those scores. Inspired by this, we introduce a post-processing framework to fully characterize multi-objective L2D solutions. Instead of the traditional staged learning approach—where a classifier is trained separately from the rejection function—we propose a joint learning method. This avoids issues such as unintended biases and fairness constraints that staged learning often fails to satisfy.
We formulate the L2D problem as a generalization of the Neyman-Pearson lemma, originally used in hypothesis testing. By extending this theorem to a multi-hypothesis setting, we derive an optimal strategy for balancing competing objectives in L2D. Our solution reframes the problem into a functional linear programming model, incorporating randomness to make it computationally feasible. We demonstrate that our post-processing algorithm generalizes well across different constraints and objectives, outperforming baseline methods in ensuring fairness. Experimental results on tabular and text datasets validate its effectiveness, while the broader implications of our approach for constrained classification problems remain open for future research.