Reinforcement Learning and Control
Model-based Reinforcement Learning and Planning
Object-centric Self-supervised Reinforcement Learning
Self-exploration of Behavior
Causal Reasoning in RL
Equation Learner for Extrapolation and Control
Intrinsically Motivated Hierarchical Learner
Regularity as Intrinsic Reward for Free Play
Curious Exploration via Structured World Models Yields Zero-Shot Object Manipulation
Natural and Robust Walking from Generic Rewards
Goal-conditioned Offline Planning
Offline Diversity Under Imitation Constraints
Learning Diverse Skills for Local Navigation
Learning Agile Skills via Adversarial Imitation of Rough Partial Demonstrations
Combinatorial Optimization as a Layer / Blackbox Differentiation
Object-centric Self-supervised Reinforcement Learning
Symbolic Regression and Equation Learning
Representation Learning
Stepsize adaptation for stochastic optimization
Probabilistic Neural Networks
Learning with 3D rotations: A hitchhiker’s guide to SO(3)
Probabilistic Neural Networks
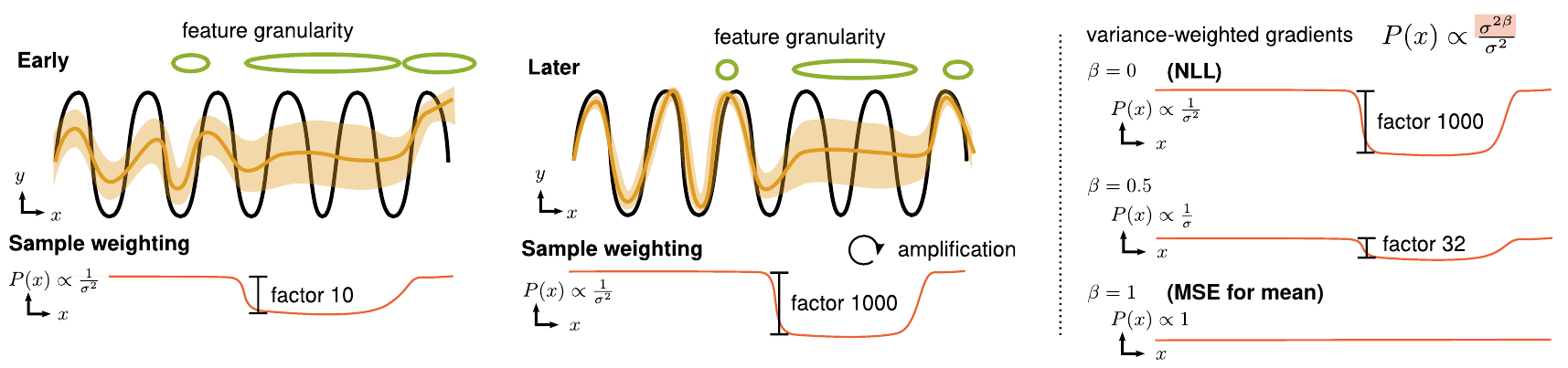
In this project, we investigate learning probabilistic neural networks, that is, neural networks that output an uncertainty-aware prediction. Specifically, we are interested in modeling aleatoric uncertainty, which is the uncertainty inherent in the data. Recognizing such uncertainties is for example useful in model-based RL or for controlled exploration.
The standard approach to modeling (heteroscedastic) aleatoric uncertainty is to predict mean and variance of a Gaussian distribution, and train the model by minimizing the negative log likelihood (NLL) of the data. In practice, this approach encounters certain optimization difficulties which lead to suboptimal predictive accuracy. In this project, we investigated the reasons behind this phenomenon and found that it is related to unequally weighted gradients across the data. We identify a simple solution, which call beta-NLL, that simply reweights the gradients in the loss. We show that the new loss leads to higher accuracy, calibrated uncertainties, is robust to hyperparameters and simple to implement.
A Pytorch implementation of the loss function:
"""Compute beta-NLL loss
:param mean: Predicted mean of shape B x D
:param variance: Predicted variance of shape B x D
:param target: Target of shape B x D
:param beta: Parameter from range [0, 1] controlling relative
weighting between data points, where `0` corresponds to
high weight on low error points and `1` to an equal weighting.
:returns: Loss per batch element of shape B
"""
loss = 0.5 * ((target - mean) ** 2 / variance + variance.log())
loss = loss * (variance.detach() ** beta)
Members
Publications

