Causal Representation Learning
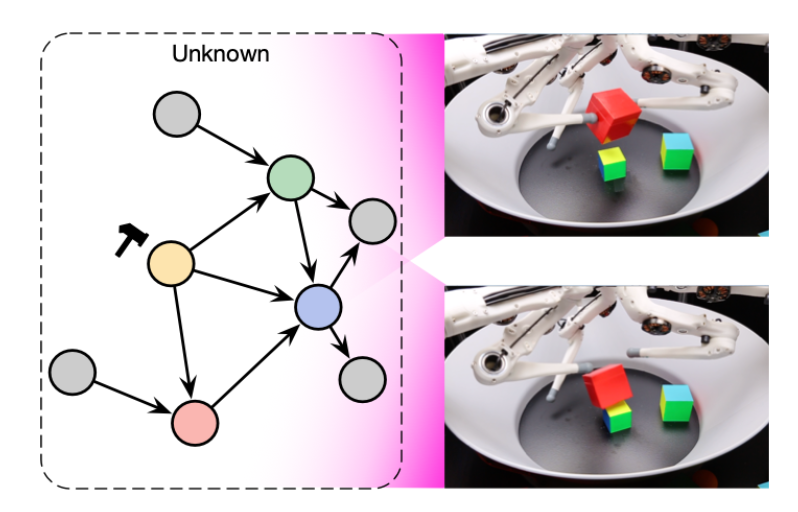
Given complex low-level data such as images or sensory inputs, causal representation learning seeks to extract the underlying high-level causal variables [].
High-dimensional data such as images are often not structured into variables that permit meaningful interventions. In this case, traditional causal methods are not applicable. One remedy is to model the raw data as transformations of a set of underlying latent variables. The goal of causal representation learning is to learn representations from data that recover the underlying latent causal variables and their structure. Such a representation can then be used for planning, to predict the effect of interventions, or for out-of-distribution generalization. We work on the theoretical foundations of causal representation learning, in particular investigating the identifiability problem: i.e., which assumptions on the data allow us to recover the latent causal structure, up to suitable (gauge) transformations. We also investigate how causal prior knowledge can be embedded into architectures and training procedures, for challenging problems like 3D reconstruction and distribution shift.
Identifying latent variable models
We previously [] introduced orthogonality of the columns of the Jacobian as an instantiation of the principle of independent mechanisms and a new notion of non-statistical independence for ICA. We extended this work by showing that in the deterministic limit, variational autoencoders are biased towards the corresponding function class of orthogonal coordinate transformations [
]. We also showed partial identifiability results for this function class [
], constituting the first such progress on a long-standing problem in nonlinear ICA. Moreover, we show that the subclass of local isometries can be approximately identified when the function class is slightly misspecified, initiating the investigation of robustness properties of identifiable representation learning [
].
Interventional Representation Learning
As non-linear representation learning is not, in general, identifiable, assumptions are necessary. We studied several settings where we have access to interventional distributions. In particular, we showed that if the latent structure is known, one intervention per node is sufficient for identifiability []. We further found that two paired interventions per node are sufficient for identifiability in the fully non-parametric setting [
], while for linear Gaussian latent structures, one intervention per node is sufficient and an efficient contrastive algorithm exists [
]. Finally, we went beyond interventional representation learning and introduced a notion of `concepts' that can be identified from diverse conditional data [
].
Disentangled representations
We developed a novel framework to assess the quality of learned `disentangled' representations that takes into account their size and explicitness []. We studied how the inductive bias of hierarchically structured autoencoders promotes disentangled representations [
], and investigated properties of learned representations through interventions in the latent space [
].
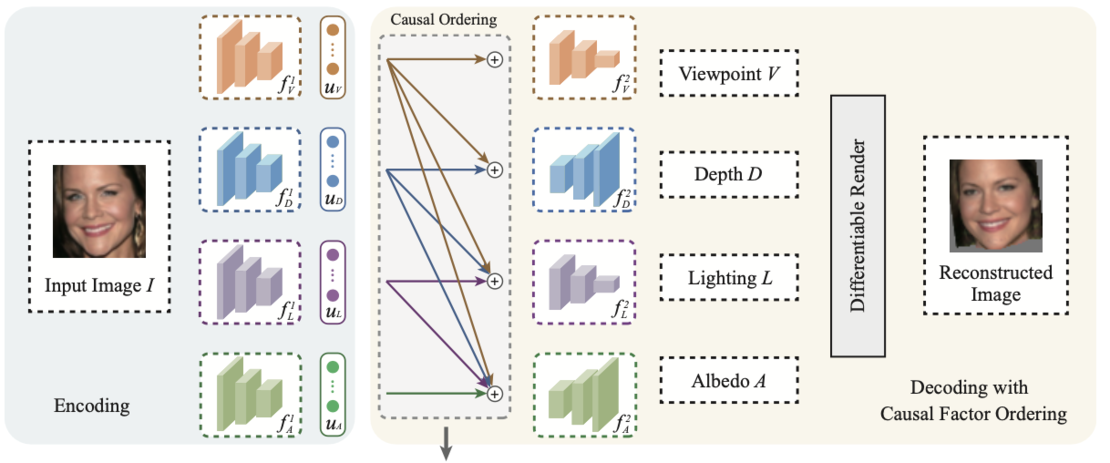
Using a flexible causal graph on high-level variables for 3D image reconstruction [].
Using causality for representation learning
3D scene reconstruction from single images is a challenging ill-posed problem. We show how causal assumptions on the topological order of variables in the latent space yields a beneficial inductive bias for reconstruction []. In an effort towards a mathematical formalization of what constitutes a causal representation if the interventions have a group structure, we have identified a homomorphism property, and shown how to learn world models that capture symmetries described by group actions [
]. Moreover, we propose a method to learn abstractions of complex systems that preserve causal information such as the effect of interventions and in particular contain information about a target variable of interest [
].
For the setting of changing environments, we propose a framework to learn invariant causal representation and prove corresponding generalization guarantees []. In the related setting of source-free domain adaption where we want to generalize to a new domain without having access to the original training data, we propose a bottom-up feature restoration method to align representations of training and new environments, thus enabling generalization [
]. Moreover, we have developed methods to interpolate between worst and average case approaches for multi-domain data using quantile regression which yields predictors that generalize with high probability [
], and we use invariant predictions as pseudo-labels to safely harness certain spurious (non-causal) features [
].