Causal models capture not just statistical dependencies, but also mechanistic ones, often involving structural causal models (SCMs). We work on the foundations of causal learning, including questions of identifiability and new frameworks for causality that address the limitations of SCMs. Moreover, we develop algorithms for causal discovery with a focus on settings with non-i.i.d.  data. Finally, we apply causality to a broad range of topics in machine learning.

Foundations of causality

While SCMs are a standard framework to model causally connected variables, they have limitations, such as difficulties in handling cyclic relations. We developed a measure-theoretic framework for causality that generalizes prior notions of causality []. Moreover, we introduced a diffusion modeling framework [] that avoids the common but often prohibitive assumption of acyclicity in causal models, which can be restrictive for modeling real-world phenomena, from the environmental sciences to genomics where feedback loops are abundant. It is generally impossible to learn causal relations without assumptions on the data distribution. We provided a new identifiability result in the bivariate case, applicable for a large class of models []. Counterfactuals are an important notion to describe hypothetical scenarios. We formalized an alternative backtracking semantics for counterfactuals [] (Best Paper Award at CLeaR 2023), which is better suited for diagnostic reasoning tasks such as root cause analysis, and developed a practical implementation for causal systems consisting of deep generative models []. 

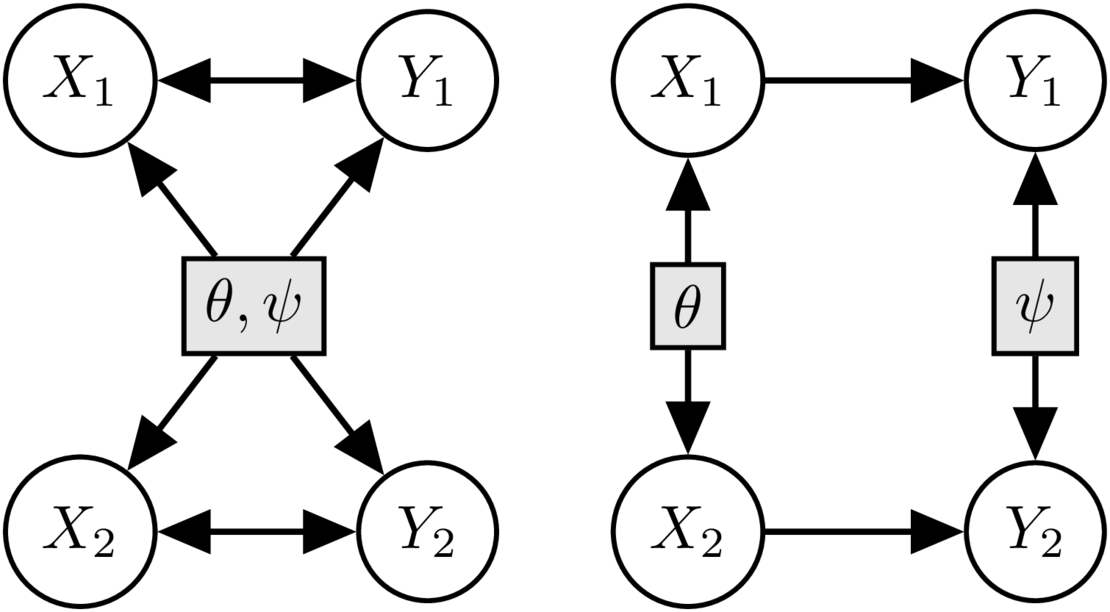
Causal inference with heterogeneous data

Standard machine learning often relies on i.i.d.\ data. We now understand, however, that non-i.i.d. data is not necessarily a problem; rather, with the right (causal) assumptions, it can be an advantage, in particular when it comes to understanding causality and out-of-distribution generalization. To this end, we provided a causal version of the classical de Finetti theorem. Subject to a formalization of our earlier  postulate of independent causal mechanism, we proved the existence of independent latent de Finetti variables that control the causal mechanisms []. This result allows us to identify an invariant causal structure underlying exchangeable non-i.i.d. data, and it provides a natural mathematical formalization of multi-environment settings. As a next step, we proved a generalized truncated factorization formula that permits both identification and estimation of causal effects from exchangeable data (Do Finetti []), presented as a NeurIPS 2024 Oral. A common assumption for multi-environment data is that environments differ in only a few mechanisms (`sparse mechanism shift' hypothesis). We showed that this assumption allows us to identify the causal structure from multi-environment data []. Sometimes we only have access to datasets that each contain information about different proper subsets of the variables, yet we are interested in a (causal or statistical) model of the joint system. We have proposed a method for merging causal sub-models [], and showed how, subject to causal assumptions and marginal information, we can recover missing information about the joint distribution for the purpose of prediction [].

Causal inference with interventional data

A special case of heterogeneous data is data corresponding to interventions, i.e., external perturbations of the data generating mechanism that affect one or few variables or mechanisms. To leverage such perturbation data, we developed a continuous optimization approach [] that allows inferring causality even when the targets and effects of the perturbations are unknown a priori, for example, in biological experiments.  Since collecting such experimental data may be costly, we developed methods for designing new perturbations that are optimally informative about aspects of the underlying system []. 

Causal discovery is a nontrivial inference problem, however, prior knowledge can help. To alleviate this, we proposed an amortized Bayesian structure learning approach [] that is pre-trained at scale on expert simulators, for example, in systems biology. We also constructed a new metric to quantify distances between causal models that accounts for the effect of interventions [].

Applying causality to machine learning

Causal concepts can help improve and understand machine learning algorithms. In [], we investigated the inner workings of trajectory prediction methods by leveraging causal feature attribution methods and links to Granger causality. Algorithmic recourse aims to provide recommendations on how to change features to alter the decision of a classifier. Since such a change constitutes an intervention and the features may be causally connected, we have argued for this to be treated as a causal problem  [].

In reinforcement learning, we provide a causal perspective on credit assignment. The advantage function can be understood as the causal effect of an action on the return, allowing us to decompose the return of a trajectory into parts caused by the agent’s actions (skill) and parts outside the agent’s control (luck). This allows us to build more efficient algorithms, and learn representations that respect the causal relationships between variables []. 

Finally, we built an instance of what we call a causal digital twin by combining mechanisms from different sources (observational, epidemiological simulation, and medical literature) into an overall causal model that allows to investigate counterfactual vaccination strategies [].