Generative Modeling

Machine learning has made significant progress in building high-dimensional generative models for real-world data. With much of the initial attention focusing on images and text, we decided to look at a less explored area and built one of the first high-performance generative models for music, both unconditional and text-to-music, enabling efficient and high-quality text-conditioned generation of music with nontrivial medium-term temporal structure [].

Our work on generating visual data focused on 3D modeling, in collaboration with vision groups in and outside our institute. Our bias towards causal and compositional models led us to explore disentangled scene graph representations, building a text-to-3D generative model [] capable of compositional 3D scene generation. To further improve the 3D generative modeling, we introduced a general expressive 3D representation []. Such a representation allows for easy incorporation of diffusion models.

For generative modeling of complex structures with specific symmetries (e.g., SE(3)-equivariance), we have developed a series of normalizing flow models []. We have also developed a PyTorch library for normalizing flows [].

Efficient Adaptation of Foundation Models

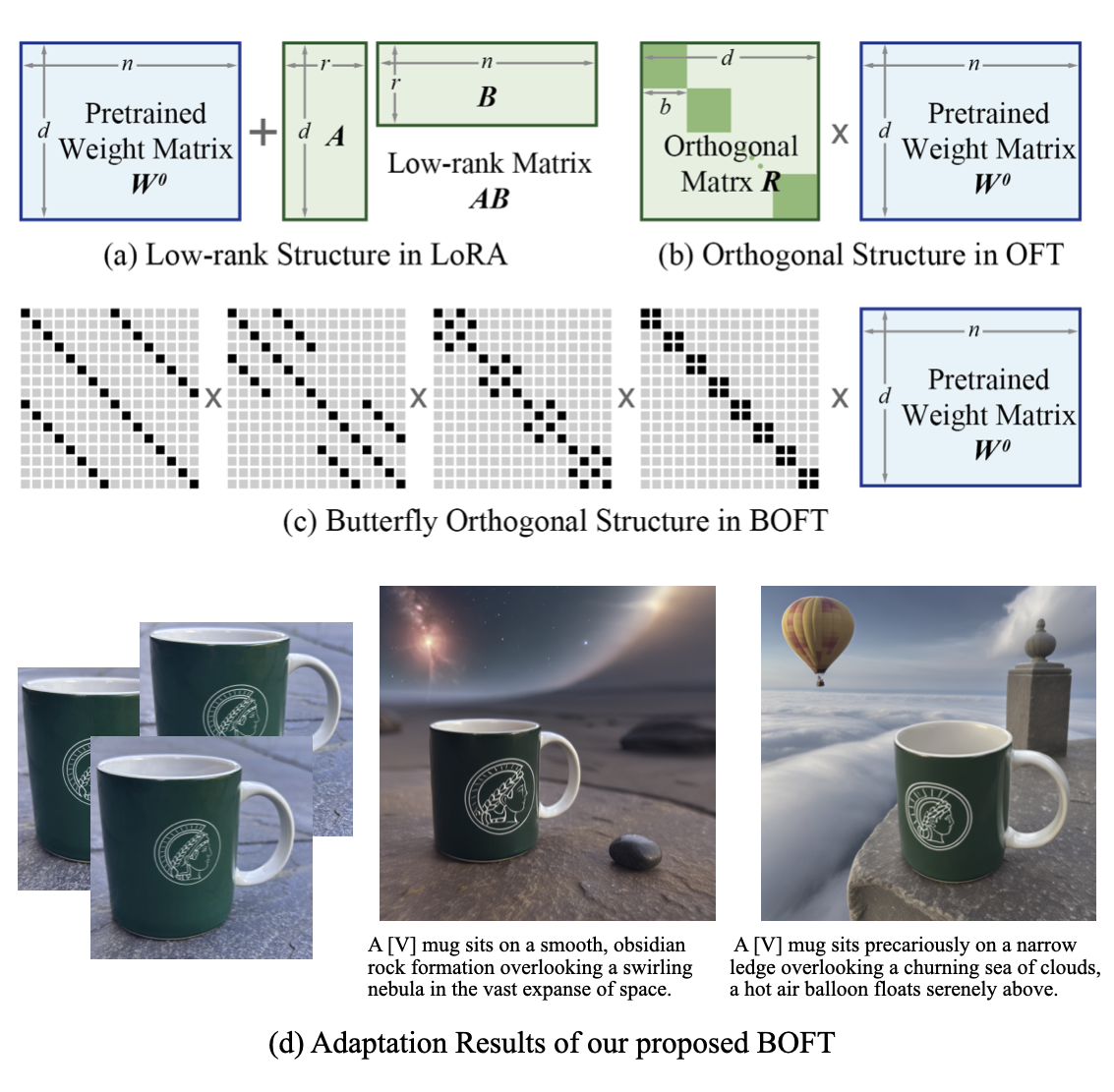
The advancement of large-scale pretrained models (foundation models) has transformed how researchers and engineers approach and solve downstream tasks, shifting from end-to-end learning to a pretraining-and-adaptation workflow. This paradigm shift makes efficient adaptation methods particularly important; moreover, adaptation is a domain where academic labs with limited compute resources can still be competitive. We have developed a family of parameter-efficient adaptation methods -- orthogonal finetuning (OFT) []. OFT enables provably stable and efficient adaptation of foundation models to downstream tasks, such as controlling text-to-image generation and solving mathematical problems. The adaptation stability of OFT can prevent the catastrophic forgetting of pretrained models, making it possible for foundation models to continually acquire novel skills. By leveraging the matrix structure of fast Fourier transform, we made OFT one of the most parameter-efficient adaptation models in practice []. This enables efficient adaptation of large language models with minimal computational overhead.

Deep Representation Learning

Learning generalizable representations remains a fundamental challenge in machine learning research. Towards this goal, we have developed a new model architecture based on a discrete bottleneck containing pairs of separate and learnable key-value codes []. To facilitate the representation learning, we propose a general framework [] to design objective functions. Different from the widely adopted cross-entropy loss that couples the two objectives of minimum intra-class variability and maximum inter-class separability, our new framework can decoupled these two objectives and model them using different characterizations. This provides a unified yet flexible way to design objective functions for representation learning.

Beyond general representation learning, we show that causal object-centric representation can be learned in an unsupervised manner from videos of scenes by exploiting the principle of common fate from Gestalt psychology []. These representations permit separate interventions on the shape, number and positions of objects.

Understanding Deep Learning from Optimization

In [], we characterize the local geometry of the loss landscape of Convolutional Neural Networks by analyzing the structure of their Hessian matrix. A key finding here was to show that the rank of the Hessian, a measure of the local dimensionality, is bounded from above by the square root of the number of parameters, extending past results to a broader family of neural networks. Our work [] derived a generalization bound for finite-width neural networks that captures the double-descent behavior of population loss with increasing network capacity. The analysis highlights the role of the rank and condition number of the Hessian at convergence in determining the generalization behavior. Along the way, this work also uncovers the vanishing Hessian behavior at the interpolation threshold and elaborates on connections to the classical leave-one-out estimator.