Reinforcement Learning and Control
Model-based Reinforcement Learning and Planning
Object-centric Self-supervised Reinforcement Learning
Self-exploration of Behavior
Causal Reasoning in RL
Equation Learner for Extrapolation and Control
Intrinsically Motivated Hierarchical Learner
Regularity as Intrinsic Reward for Free Play
Curious Exploration via Structured World Models Yields Zero-Shot Object Manipulation
Natural and Robust Walking from Generic Rewards
Goal-conditioned Offline Planning
Offline Diversity Under Imitation Constraints
Learning Diverse Skills for Local Navigation
Learning Agile Skills via Adversarial Imitation of Rough Partial Demonstrations
Combinatorial Optimization as a Layer / Blackbox Differentiation
Object-centric Self-supervised Reinforcement Learning
Symbolic Regression and Equation Learning
Representation Learning
Stepsize adaptation for stochastic optimization
Probabilistic Neural Networks
Learning with 3D rotations: A hitchhiker’s guide to SO(3)
Bayesian Optimization
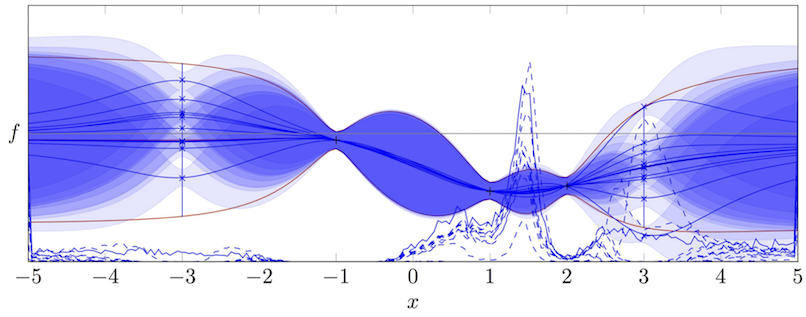
Bayesian Optimization is an increasingly popular approach to industrial and scientific prototyping problems. The basic premise in this setting is that one is looking for a location $x$ in some domain where a fitness function $f(x)$ is (globally) minimized. The additional, sometimes implicit, assumption is that individual evaluations of $f$ have comparably high computational or monetary cost (e.g. because they involve building a physical prototype, or running a robot for a few minutes). To avoid this high cost as much as possible, one thus builds a cheaper surrogate model for the true objective. If this model is probabilistic (i.e. it spreads probability mass over a space of possible true values of the objective) it can be used to reason about which physical experiments would be most useful to perform in pursuit of the true extremum.
Our contribution to this area is the development of a class of Bayesian optimization algorithms, known as Entropy Search [] that retain an explicit model for the location of a function's minimum, and reason about changes to this distribution effected by future experiments. Entropy Search is not a cheap method, but it provides a powerful representation in which one can reason about the information content of various kinds of experiments, and take decisions that take into account varying costs and quality of potential experiments.
In recent years, in collaboration with the Intelligent Control Systems group, the Entropy Search framework has been used to build advanced functionality for experimental design in automated machine learning and robotics. This includes the ability to simultaneously and efficiently use and trade off experimental channels of varying fidelity and cost [], and the effective use of strong analytical knowledge about a problem [
].
Members
Publications



